|
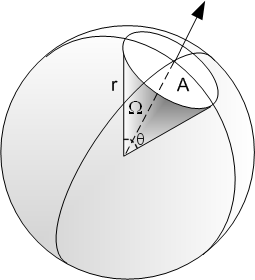
Un angle solide est l'analogue en 3 dimensions de l'angle plan en 2 dimensions.
L'angle solide Ω est égal au rapport de la surface A observée divisée par le carré de la distance d'observation r.
Ω=A/r^2
Il est exprimé en stéradian (sr), unité du système international. Il est compris en 0 et 4π sr pour la sphère entière.
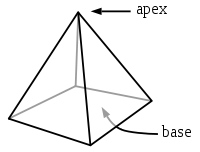
Pour un cône régulier, l'angle solide Ω est égal à Ω =2 π x (1 - cos(θ/2))
où θ est l'angle plan de l'apex du cône (c'est à dire l'angle quand on sectionne le cône). Par exemple, une hémisphère (demie boule) correspond à un angle plan θ de π rd (180 °) et un angle solide de 2π sr
Si on inverse la formule précédente, on peut déduire l'angle plan θ à partir de l'angle solide Ω :
θ = 2 x arccos(1- Ω/2π)
Par exemple, le diamètre apparent de la Lune vue de la Terre est de θ=0.5 °, ce qui correspond à un angle solide d'environ 6e-5 stéradian.
Le champ de lecture avec les yeux est de θ=3 ° (0.002 sr) (zone fovéale).
Le champ de vision de veille attentive avec les yeux est d'environ θ=25 ° (forme d'ellipse avec -15° gauche, +15 ° droite, -8° haut, +12° bas) soit environ 0.15 sr.
Le champ suivant représente l'angle solide Ω du cône régulier dont l'angle plan θ figure au tableau du haut.
|


 Accueil mon-convertisseur.fr
Accueil mon-convertisseur.fr Convertisseur de distance
Convertisseur de distance Convertisseur de poids
Convertisseur de poids Convertisseur vitesse
Convertisseur vitesse Convertisseur température
Convertisseur température Convertisseur durée
Convertisseur durée Convertisseur pression
Convertisseur pression Convertisseur RIB vers IBAN
Convertisseur RIB vers IBAN Bois de chauffage
Bois de chauffage Calculateur clé numéro sécurité sociale
Calculateur clé numéro sécurité sociale Conversion de devises
Conversion de devises Convertisseur surface
Convertisseur surface Calculateur inflation
Calculateur inflation Calculateur numéro SIRET, TVA
Calculateur numéro SIRET, TVA Conversion d'angle
Conversion d'angle Convertisseur de volume
Convertisseur de volume Estimation espérance de vie
Estimation espérance de vie Convertisseur de puissance
Convertisseur de puissance Calcul indice de masse corporelle
Calcul indice de masse corporelle Recherche de code postal
Recherche de code postal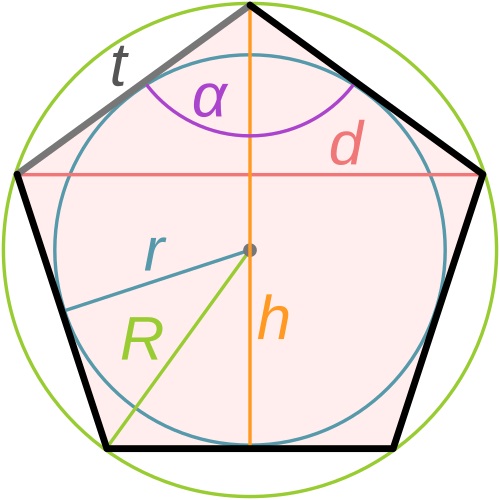 Pentagone
Pentagone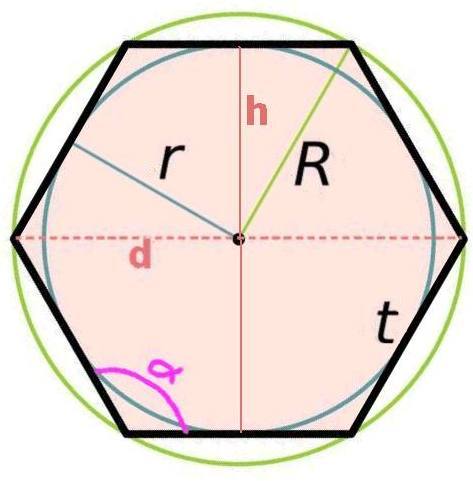 Hexagone
Hexagone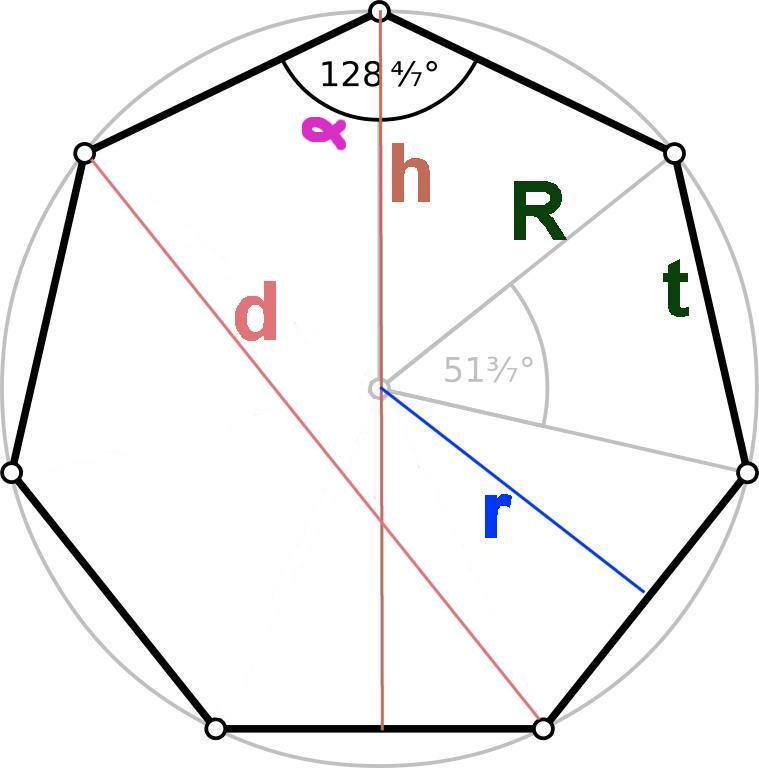 Heptagone
Heptagone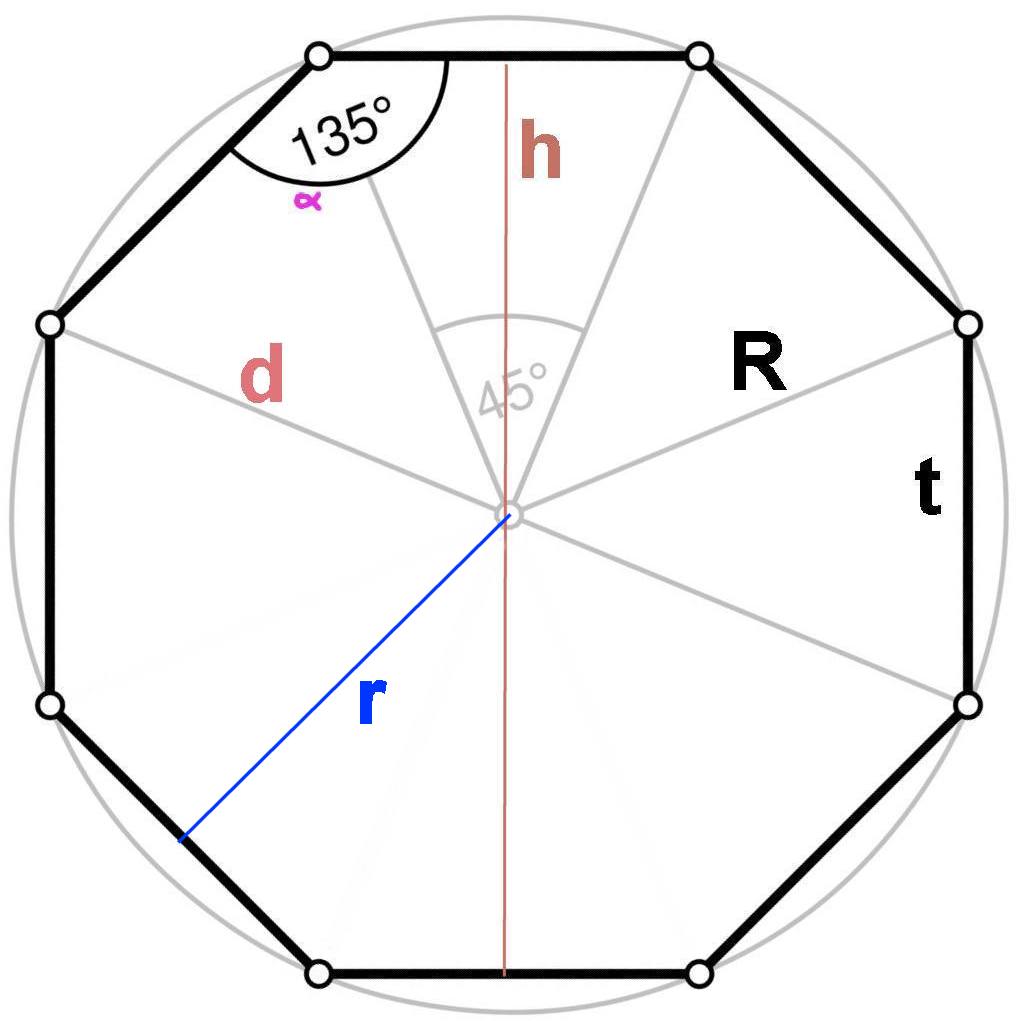 Octogone
Octogone Quiz Code Route
Quiz Code Route QCM anglais
QCM anglais Conversion devises dans le passé
Conversion devises dans le passé Graphique de cours de change historique
Graphique de cours de change historique Solveur Sokoban
Solveur Sokoban